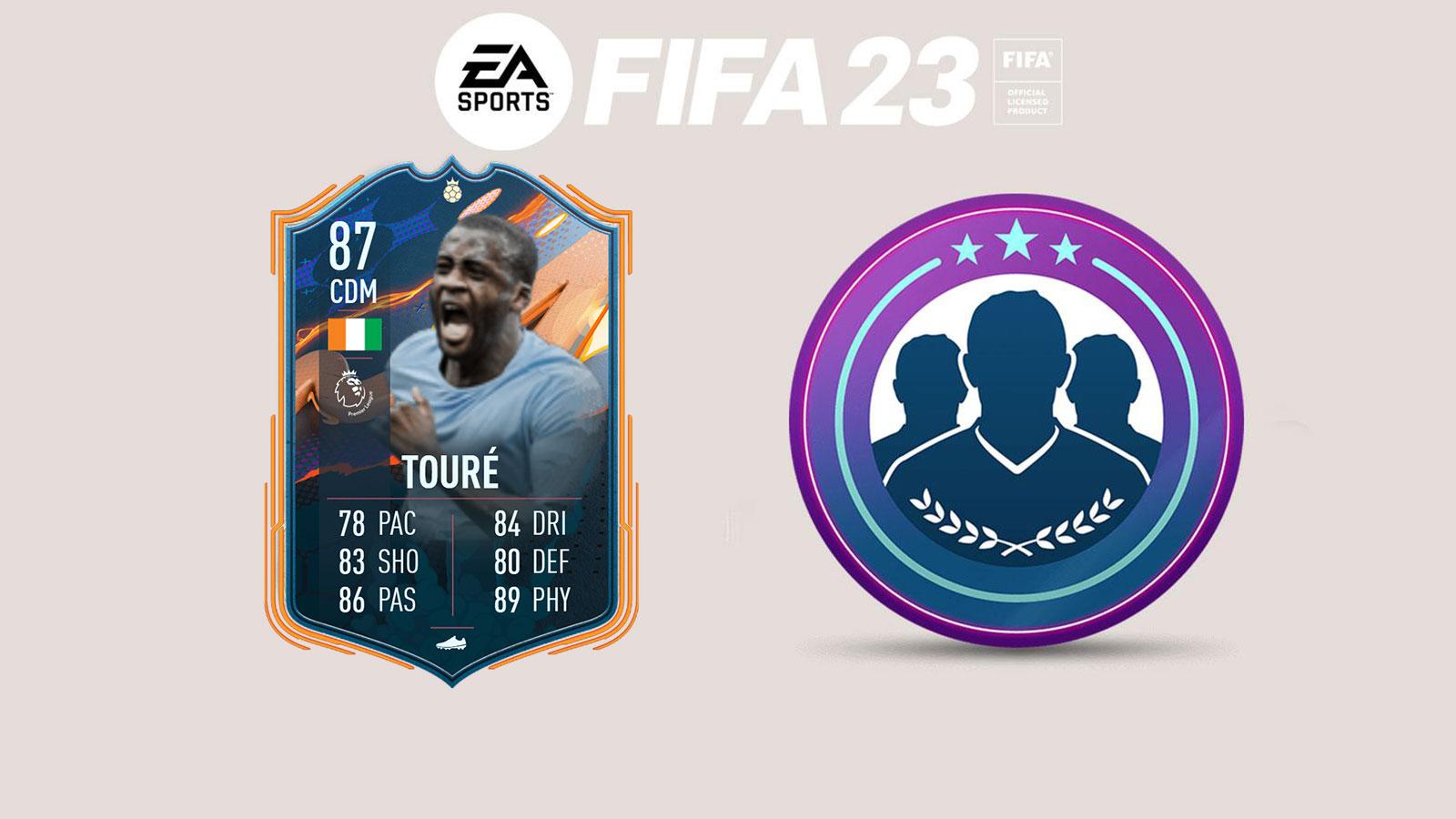
Solution DCE Vidal Flashback la moins chère possible sur FIFA 19

Un nouveau type de DCE (Défis de Création d’Equipe) est disponible cette année sur FUT. Découvrez la solution ci-dessous.
Découvrez tout d’abord l’équipe de l’événement FUT Birthday qui a modifié les postes de nombreux joueurs avec notamment Van Dijk BU ou encore Ibrahimovic DC.
Comme depuis plusieurs années maintenant, le mode FUT contient des DCE qui incitent les joueurs à devoir réussir plusieurs défis afin d’obtenir des récompenses comme des packs, des crédits ou des cartes spéciales.
Cette année, les éléments Flashback qui sont des cartes boostées des joueurs, qui ont été performants lors de ces dernières années, sont disponibles.
Aujourd’hui, nous vous proposons la solution du DCE Flashback Vidal qui a pour récompense une carte boost d’Arturo Vidal avec 89 de général.
Ce challenge se termine le mercredi 27 mars à 19h.
Solution La Roja :
- Joueurs – Chili : Minimum 1
- Joueurs – Equipe de la Semaine : Minimum 2
- Note de l’équipe : Minimum 83
- Collectif : Minimum 75
- Nombre de joueurs : 11
-> Récompense : Pack Joueurs Or Premium
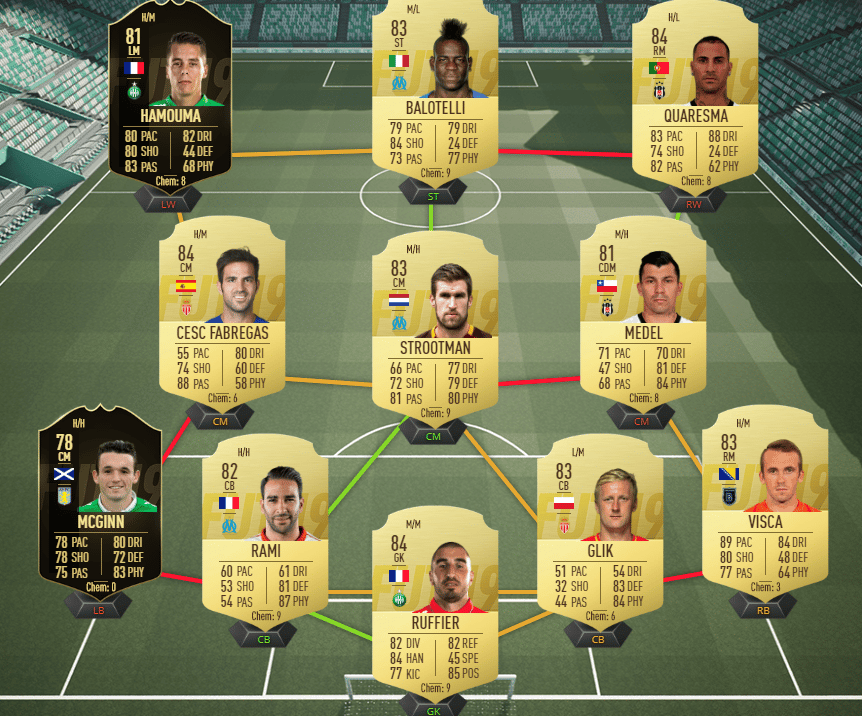
PS4 : 46 050 crédits
Xbox One : 43 250 crédits
• Lire aussi : Les cartes MOTM (Hommes du match) sur FIFA 19
Solution Bayern Munich :
- Joueurs – Bayern Munich : Minimum 1
- Joueurs – Equipe de la Semaine : Minimum 1
- Note de l’équipe : Minimum 86
- Collectif : Minimum 65
- Nombre de joueurs : 11
-> Récompense : Pack Joueurs Rare
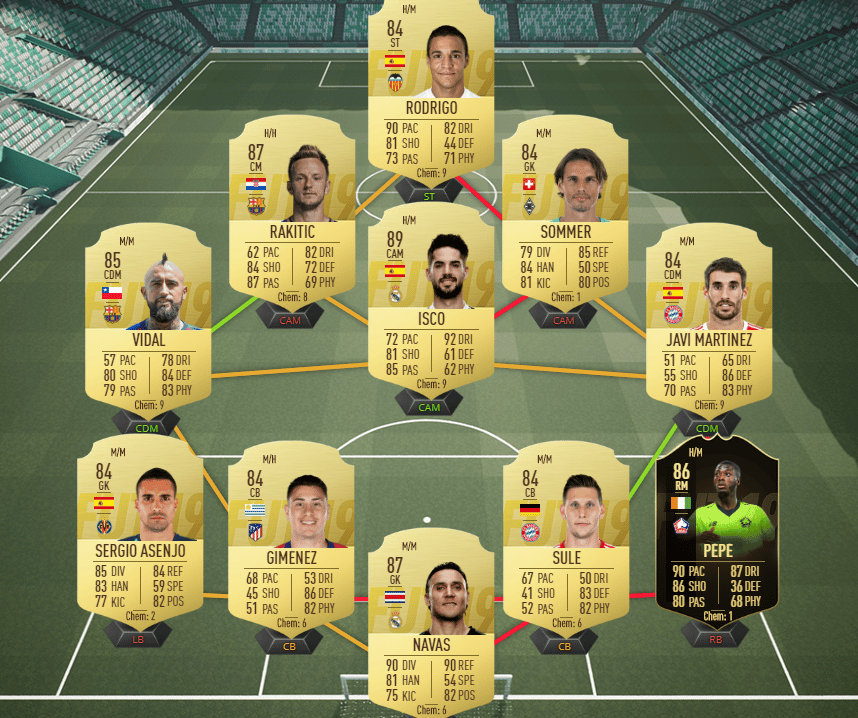
PS4 : 177 700 crédits
Xbox One : 175 300 crédits
Solution Equipe 85 :
- Joueurs – Equipe de la Semaine : Minimum 2
- Note de l’équipe : Minimum 85
- Collectif : Minimum 70
- Nombre de joueurs : 11
-> Récompense : Pack Mega Rare
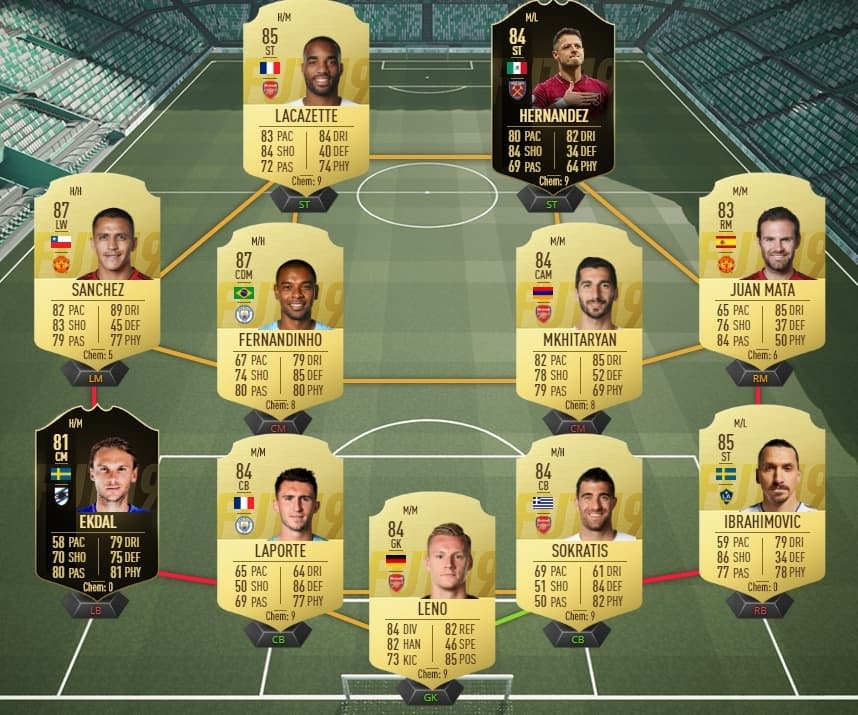
PS4 : 131 300 crédits
Xbox One : 129 700 crédits
Si vous voulez d’autres solutions de DCE, cliquez ici !